Advertisements
Advertisements
प्रश्न
In the following figure, a circle is inscribed in the quadrilateral ABCD.

If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
उत्तर
From the figure we see that BQ = BR = 27 cm ...(Since length of the tangent segments from an external point are equal)
As BC = 38 cm
`=>` CR = CB − BR
= 38 − 27
= 11 cm
Again,
CR = CS = 11 cm ...(Length of tangent segments from an external point are equal)
Now, as DC = 25 cm
∴ DS = DC − SC
= 25 − 11
= 14 cm
Now, in quadrilateral DSOP,
∠PDS = 90° ...(Given)
∠OSD = 90°, ∠OPD = 90° ...(Since tangent is perpendicular to the
radius through the point of contact)
`=>` DSOP is a parallelogram
`=>` OP || SD and PD || OS
Now, as OP = OS ...(Radii of the same circle)
`=>` OPDS is a square.
∴ DS = OP = 14 cm
∴ Radius of the circle = 14 cm
APPEARS IN
संबंधित प्रश्न
The radius of a circle is 17.0 cm and the length of perpendicular drawn from its centre to a chord is 8.0 cm. Calculate the length of the chord.
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords, if both the chords are
(i) on the opposite sides of the centre,
(ii) on the same side of the centre.
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centres of
the circles. Show that:
(i) AB = CD,
(ii) AC = BD.

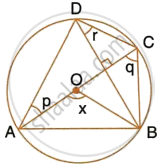
In the given figure, AC is a diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q and r in terms of x.
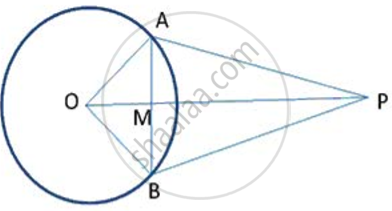
From a point P outside a circle, with centre O. tangents PA and PB are drawn as following fig., Prove that ∠ AOP = ∠ BOP and OP is the perpendicular bisector of AB.
A chord of length 8 cm is drawn at a distance of 3 cm from the center of the circle.
Calculate the radius of the circle.
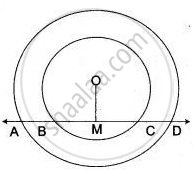
The figure shows two concentric circles and AD is a chord of a larger circle.
Prove that: AB = CD.
M and N are the mid-points of two equal chords AB and CD respectively of a circle with center O.
Prove that: (i) ∠BMN = ∠DNM
(ii) ∠AMN = ∠CNM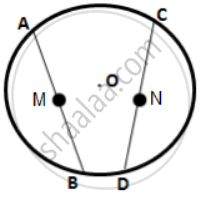
In the given figure, l is a line intersecting the two concentric circles, whose common center is O, at the points A, B, C, and D. Show that AB = CD.
In Fig. O is the centre of the circle with radius 5 cm. OP⊥ AB, OQ ⊥ CD, AB || CD, AB = 8 cm and CD = 6 cm. Determine PQ.