Advertisements
Advertisements
प्रश्न
In the following figure, a circle is inscribed in the quadrilateral ABCD.

If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
उत्तर
From the figure we see that BQ = BR = 27 cm ...(Since length of the tangent segments from an external point are equal)
As BC = 38 cm
`=>` CR = CB − BR
= 38 − 27
= 11 cm
Again,
CR = CS = 11 cm ...(Length of tangent segments from an external point are equal)
Now, as DC = 25 cm
∴ DS = DC − SC
= 25 − 11
= 14 cm
Now, in quadrilateral DSOP,
∠PDS = 90° ...(Given)
∠OSD = 90°, ∠OPD = 90° ...(Since tangent is perpendicular to the
radius through the point of contact)
`=>` DSOP is a parallelogram
`=>` OP || SD and PD || OS
Now, as OP = OS ...(Radii of the same circle)
`=>` OPDS is a square.
∴ DS = OP = 14 cm
∴ Radius of the circle = 14 cm
APPEARS IN
संबंधित प्रश्न
AB and CD are two parallel chords of a circle such that AB = 24 cm and CD = 10 cm. If the
radius of the circle is 13 cm. find the distance between the two chords.

Two circle with centres A and B, and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q; find the length of PQ.
In following figure , AB , a chord of the circle is of length 18 cm. It is perpendicularly bisected at M by PQ.
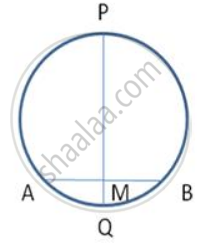
The figure shows two concentric circles and AD is a chord of a larger circle.
Prove that: AB = CD.
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centers of the circles.
Show that:
(i) AB = CD ;
(ii) AC = BD.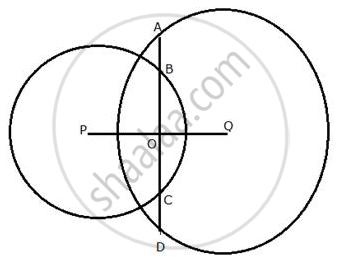
In the following figure; P and Q are the points of intersection of two circles with centers O and O'. If straight lines APB and CQD are parallel to OO';
prove that: (i) OO' = `1/2`AB ; (ii) AB = CD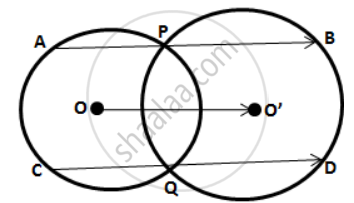
Two chords AB and CD of a circle are parallel and a line L is the perpendicular bisector of AB. Show that L bisects CD.
Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 13 cm.
AB is a diameter of a circle with centre O and radius OD is perpendicular to AB. If C is any point on arc DB, find ∠ BAD and ∠ ACD.
AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.
