Advertisements
Advertisements
प्रश्न
AB and CD are two parallel chords of a circle such that AB = 24 cm and CD = 10 cm. If the
radius of the circle is 13 cm. find the distance between the two chords.

उत्तर
Join OA and OC.
Since the perpendicular from the centre of the circle to a chord bisects the chord.
Therefore, N and M are the mid-points of AB and CD respectively.
Consequently
`AN = NB = 1/2 AB = 1/2 xx 24 = 12` cm and
`CM = MD = 1/2 CD = 1/2 xx 10` = 5 cm
In right-angled triangles ANO and CMO, we have
OA2 = ON2 + AN2 and OC2 = OM2 + CM2
⇒ 132 = ON2 + 122 and 132 = OM2 + 52
⇒ ON2 = 132 - 122 and OM2 = 132 - 52
⇒ ON2 = 169 - 144 and OM2 = 169 - 25
⇒ ON2 = 25 and OM2 = 144
⇒ ON = 5 and OM = 12
Now, NM = ON + OM = 5 + 12 = 17cm
Hence, the distance between the two chords is 17 cm.

APPEARS IN
संबंधित प्रश्न
The figure given below, shows a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4cm, find the radius of the circle.
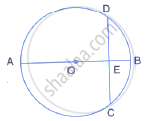
Two circle with centres A and B, and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q; find the length of PQ.
The given figure shows two circles with centres A and B; and radii 5 cm and 3 cm respectively, touching each other internally. If the perpendicular bisector of AB meets the bigger circle in P and Q, find the length of PQ.

In the following figure, a circle is inscribed in the quadrilateral ABCD.

If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
OP is the ⊥ bisector of chord AB.
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other.
If ∠MAD = x and ∠BAC = y : express ∠ABD in terms of y.

A chord of length 24 cm is at a distance of 5 cm from the center of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the center.
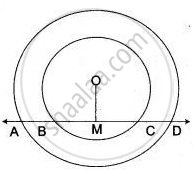
In the given figure, l is a line intersecting the two concentric circles, whose common center is O, at the points A, B, C, and D. Show that AB = CD.
The radius of a circle is 13 cm and the length of one of its chord is 10 cm. Find the distance of the chord from the centre.
AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.
