Advertisements
Advertisements
प्रश्न
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
OP is the ⊥ bisector of chord AB.
उत्तर
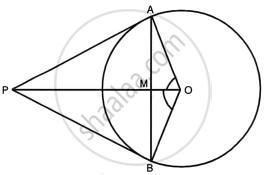
In ΔOAM and ΔOBM
OA = OB ...(Radii of the same circle)
∠AOM = ∠BOM ...(Proved ∠AOP = ∠BOP)
OM = OM ...(Common)
∴ By Side – Angle – Side criterion of congruence,
ΔOAM ≅ ΔOBM
The corresponding parts of the congruent triangles are congruent.
`=>` AM = MB
And ∠OMA = ∠OMB
But, ∠OMA + ∠OMB = 180°
∴ ∠OMA = ∠OMB = 90°
Hence, OM or OP is the perpendicular bisector of chord AB.
APPEARS IN
संबंधित प्रश्न
A chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
A chord CD of a circle whose centre is O, is bisected at P by a diameter AB.
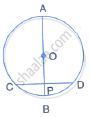
Given OA = OB = 15 cm and OP = 9 cm. calculate the length of:
(i) CD (ii) AD (iii) CB
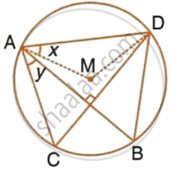
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other. If ∠MAD = x and ∠BAC = y :
- express ∠AMD in terms of x.
- express ∠ABD in terms of y.
- prove that : x = y.
In the following figure, a circle is inscribed in the quadrilateral ABCD.

If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
A chord of length 8cm is drawn inside a circle of radius 6cm. Find the perpendicular distance of the chord from the centre of the circle.
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other.
If ∠MAD = x and ∠BAC = y : express ∠ABD in terms of y.

The figure shows two concentric circles and AD is a chord of a larger circle.
Prove that: AB = CD.
In the following figure; P and Q are the points of intersection of two circles with centers O and O'. If straight lines APB and CQD are parallel to OO';
prove that: (i) OO' = `1/2`AB ; (ii) AB = CD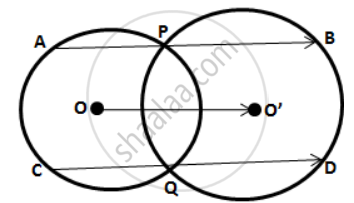
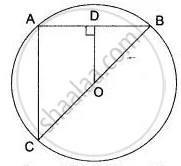
In the given figure, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2 OD.
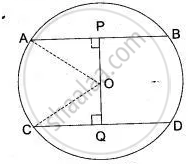
In Fig. O is the centre of the circle with radius 5 cm. OP⊥ AB, OQ ⊥ CD, AB || CD, AB = 8 cm and CD = 6 cm. Determine PQ.