Advertisements
Advertisements
प्रश्न
A chord of length 24 cm is at a distance of 5 cm from the center of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the center.
उत्तर
Let AB be the chord of length 24 cm and O be the center of the circle.
Let OC be the perpendicular drawn from O to AB.
We know, that the perpendicular to a chord, from the center of a circle, bisects the chord.
∴ AC = CB = 12 cm
In OCA,
OA2 = OC2 + AC2 ....( By Pythagoras theorem )
=(5)2 + ( 12 )2 = 169
⇒ OA = 13 cm
∴ radius of the circle = 13 cm.
Let A ' B ' be the new chord at a distance of 12 cm from the center.
∴ ( OA' )2 = ( OC' )2 + ( A'C' )2
⇒ ( A'C' )2 = ( 13 )2 - ( 12 )2 = 25
∴ A'C' = 5 cm
Hence, length of the new chord = 2 x 5 = 10 cm.
APPEARS IN
संबंधित प्रश्न
A chord CD of a circle whose centre is O, is bisected at P by a diameter AB.
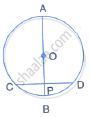
Given OA = OB = 15 cm and OP = 9 cm. calculate the length of:
(i) CD (ii) AD (iii) CB
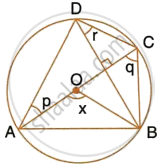
In the given figure, AC is a diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q and r in terms of x.
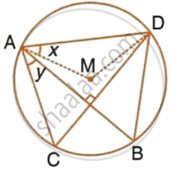
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other. If ∠MAD = x and ∠BAC = y :
- express ∠AMD in terms of x.
- express ∠ABD in terms of y.
- prove that : x = y.
In Δ ABC, the perpendicular from vertices A and B on their opposite sides meet (when produced) the circumcircle of the triangle at points D and E respectively. Prove that: arc CD = arc CE
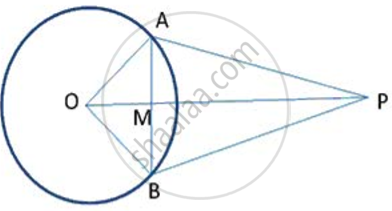
From a point P outside a circle, with centre O. tangents PA and PB are drawn as following fig., Prove that ∠ AOP = ∠ BOP and OP is the perpendicular bisector of AB.
A chord CD of a circle whose center is O is bisected at P by a diameter AB. Given OA = OB = 15 cm and OP = 9 cm.
Calculate the lengths of: (i) CD ; (ii) AD ; (iii) CB.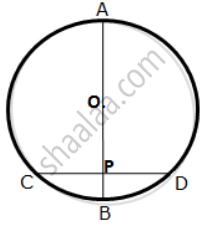
The figure shows two concentric circles and AD is a chord of a larger circle.
Prove that: AB = CD.
In the given figure, O is the center of the circle with radius 20 cm and OD is perpendicular to AB. If AB = 32 cm,
find the length of CD.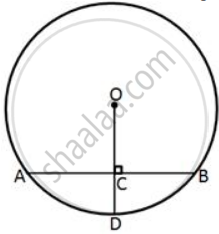
In Fig. O is the centre of the circle with radius 5 cm. OP⊥ AB, OQ ⊥ CD, AB || CD, AB = 8 cm and CD = 6 cm. Determine PQ.
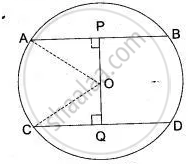
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.