Advertisements
Advertisements
प्रश्न
A chord CD of a circle whose center is O is bisected at P by a diameter AB. Given OA = OB = 15 cm and OP = 9 cm.
Calculate the lengths of: (i) CD ; (ii) AD ; (iii) CB.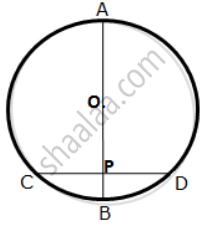
उत्तर
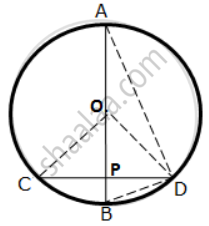
(i) OP ⊥ CD
∴ OP bisects CD. ....( Perpendicular drawn from the centre of a circle to a chord bisects it. )
⇒ CP = `"CD"/2`
In right ΔOPC,
OC2 = OP2 + CP2
⇒ CP2 = OC2 - OP2
⇒ 152 - 92 = 144
∴ CP = 12 cm
∴ CD = 12 x 2 = 24 cm
(ii) Join BD,
∴ BP = OB - OP = 15 - 9 = 6 cm.
In right ΔBPD,
BD2 = BP2 + PD2
= 62 + 122 = 180
In ΔADB,
∠ADB = 90° ...( Angle in a semi-circle is a right angle )
∴ AB2 = AD2 + BD2
⇒ AD2 = AB2 - BD2
= 302 - 180 = 720
∴ AD = `sqrt(720)` = 26.83 cm
(iii) Also, BC = BD = `sqrt(180)` = 13.42 cm.
APPEARS IN
संबंधित प्रश्न
A chord CD of a circle whose centre is O, is bisected at P by a diameter AB.
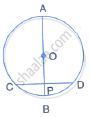
Given OA = OB = 15 cm and OP = 9 cm. calculate the length of:
(i) CD (ii) AD (iii) CB
Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the bisector of angle BAC.
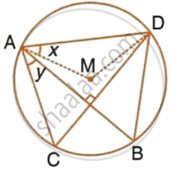
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other. If ∠MAD = x and ∠BAC = y :
- express ∠AMD in terms of x.
- express ∠ABD in terms of y.
- prove that : x = y.
PQ and QR are two equal chords of a circle. A diameter of the circle is drawn through Q . Prove that the diameter bisects ∠ PQR.
In the given figure, O is the center of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm, 
Find the :
(i) the radius of the circle
(ii) length of chord CD.
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm;
find the length of another chord.
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centers of the circles.
Show that:
(i) AB = CD ;
(ii) AC = BD.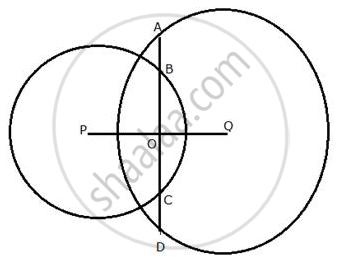
In the following figure; P and Q are the points of intersection of two circles with centers O and O'. If straight lines APB and CQD are parallel to OO';
prove that: (i) OO' = `1/2`AB ; (ii) AB = CD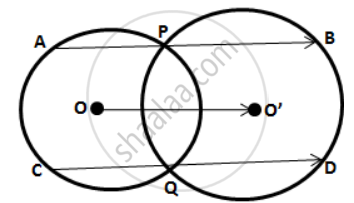
In a circle of radius 10 cm, AB and CD are two parallel chords of lengths 16 cm and 12 cm respectively.
Calculate the distance between the chords, if they are on:
(i) the same side of the center.
(ii) the opposite sides of the center.
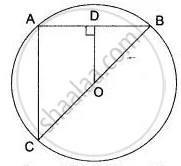
In the given figure, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2 OD.