Advertisements
Advertisements
प्रश्न
Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the bisector of angle BAC.
उत्तर
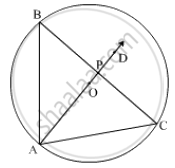
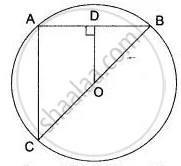
Given: AB and AC are two equal chords of C (O, r).
To prove: Centre, O lies on the bisector of ∠BAC.
Construction: Join BC. Let the bisector of ∠BAC intersects BC in P.
Proof:
In ΔAPB and ΔAPC,
AB = AC ...(Given)
∠BAP = ∠CAP ...(Given)
AP = AP ...(Common)
∴ ΔAPB ≅ ΔAPC ...(SAS congruence criterion)
`=>` BP = CP and ∠APB = ∠APC ...(CPCT)
∠APB + ∠APC = 180° ...(Linear pair)
`=>` 2∠APB = 180° ...(∠APB = ∠APC)
`=>` ∠APB = 90°
Now, BP = CP and ∠APB = 90°
∴ AP is the perpendicular bisector of chord BC.
`=>` AP passes through the centre, O of the circle.
APPEARS IN
संबंधित प्रश्न
A chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
Two circle with centres A and B, and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q; find the length of PQ.
In Δ ABC, the perpendicular from vertices A and B on their opposite sides meet (when produced) the circumcircle of the triangle at points D and E respectively. Prove that: arc CD = arc CE
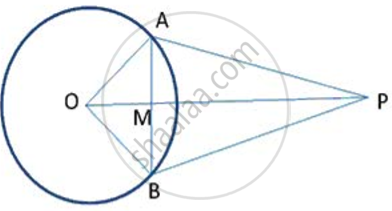
From a point P outside a circle, with centre O. tangents PA and PB are drawn as following fig., Prove that ∠ AOP = ∠ BOP and OP is the perpendicular bisector of AB.
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centers of the circles.
Show that:
(i) AB = CD ;
(ii) AC = BD.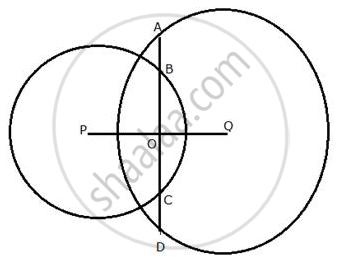
In the given figure, O is the center of the circle with radius 20 cm and OD is perpendicular to AB. If AB = 32 cm,
find the length of CD.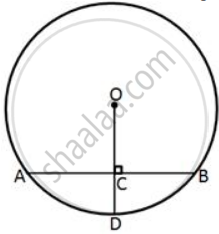
In a circle of radius 10 cm, AB and CD are two parallel chords of lengths 16 cm and 12 cm respectively.
Calculate the distance between the chords, if they are on:
(i) the same side of the center.
(ii) the opposite sides of the center.
In the given figure, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2 OD.
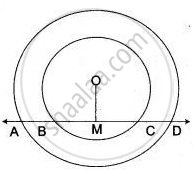
In the given figure, l is a line intersecting the two concentric circles, whose common center is O, at the points A, B, C, and D. Show that AB = CD.
Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 13 cm.
