Advertisements
Advertisements
प्रश्न
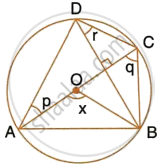
In the given figure, AC is a diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q and r in terms of x.
उत्तर

∵ Arc subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴ ∠AOB = 2∠ACB
`\implies` x = 2q
`\implies q = x/2`
But ∠ADB and ∠ACB are in the same segment
∴ ∠ADB = ∠ACB = q
Now in ΔAED.
p + q + 90° = 180° ...(Sum of angles of a Δ)
p + q = 90°
p = 90° – q
`p = 90^circ - x/2`
∵ Arc BC subtends ∠BOC at the centre and ∠ADC at the remaining part of the circle
∴ ∠BOC = 2∠BDC = 2r
∴ `r = 1/2 ∠BOC = 1/2 (180^circ - x)`
∵ (∠AOB + ∠BOC = 180°)
∴ `r = 90^circ - 1/2 x`
= `90^circ - x/2`
APPEARS IN
संबंधित प्रश्न
The radius of a circle is 17.0 cm and the length of perpendicular drawn from its centre to a chord is 8.0 cm. Calculate the length of the chord.
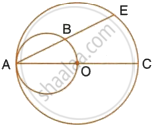
In the given figure, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that : AB = BE.
PQ and QR are two equal chords of a circle. A diameter of the circle is drawn through Q . Prove that the diameter bisects ∠ PQR.
A chord of length 8 cm is drawn at a distance of 3 cm from the center of the circle.
Calculate the radius of the circle.
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords,
if both the chords are:
(i) on the opposite sides of the centre;
(ii) on the same side of the centre.
In the given figure, O is the center of the circle with radius 20 cm and OD is perpendicular to AB. If AB = 32 cm,
find the length of CD.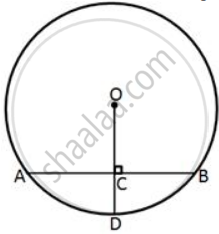
In a circle of radius 10 cm, AB and CD are two parallel chords of lengths 16 cm and 12 cm respectively.
Calculate the distance between the chords, if they are on:
(i) the same side of the center.
(ii) the opposite sides of the center.
Two chords AB and CD of a circle are parallel and a line L is the perpendicular bisector of AB. Show that L bisects CD.
AB is a diameter of a circle with centre O and radius OD is perpendicular to AB. If C is any point on arc DB, find ∠ BAD and ∠ ACD.
In Fig. O is the centre of the circle of radius 5 cm. OP ⊥ AB, OQ ⊥ CD, AB || CD, AB = 6 cm and CD = 8 cm. Determine PQ.

