Advertisements
Advertisements
प्रश्न
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

उत्तर
i. AB is a diameter.
∴ ∠ACB = 90°
The angle in a semicircle is the right angle.
∴ In ΔACB,
∠A + ∠C + ∠B = 180°
34° + 90° + ∠B = 180°
∠B = 180° – (34° + 90°)
∠B = 180° – 124°
∠B = 56°
ii. Now,
CQ is tangent.
∴ ∠QCB = ∠CAB ...(Alternate segment angle)
∴ ∠QCB = 34°
And ∠CBQ = 180° – ∠CBA
∠CBQ = 180° – 56° = 124°
∴ ∠CQA = 180° – (∠QCB + ∠CBQ)
∠CQA = 180° – (34° + 124°)
∠CQA = 180° – 158° = 22°.
APPEARS IN
संबंधित प्रश्न
In the following figure; If AB = AC then prove that BQ = CQ.

In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

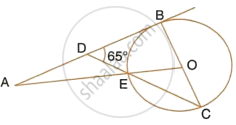
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
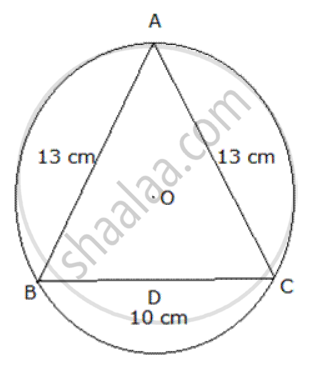
In figure , ABC is an isosceles triangle inscribed in a circle with centre O such that AB = AC = 13 cm and BC = 10 cm .Find the radius of the circle.
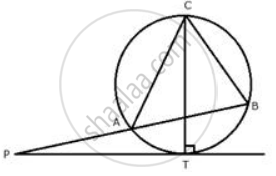
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

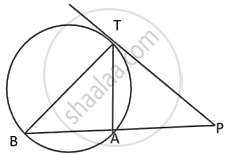
In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB
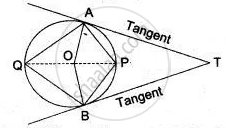
The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ:
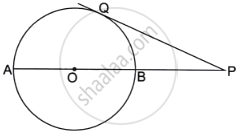
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.