Advertisements
Advertisements
प्रश्न
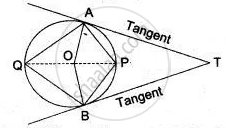
In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB
उत्तर
(i) ∠ AQP = ∠ PAT = 35° ....( Angles are in alternate segment)
(ii) ∠ BQP = ∠ PBT = 40° ....( Angles are in alternate segment)
(iii) ∠ AQB = ∠ AQP + ∠ BQP
∠ AQB = 35° + 40° = 75°
(iv) ∠ APB + ∠ AQB = 180° ....(Opposite ∠s of a cyclic quadrilateral are supplementary)
∴ ∠ APB + 75° = 180°
∴ ∠ APB = 105°
(v) ∠ AOB = 2∠ AQB = 2(75°) = 150° ....(Angle at the centre = 2 Angle at the circumference)
(vi) In quadrilateral AOBT:
∠ ATB = 360° - (∠OAT + ∠OBT + ∠AOB)
∠ ATB = 360° - (90° + 15° + 90°) = 30° ....(∠OAT = ∠OBT = 90° radius, ⊥ tangent).
APPEARS IN
संबंधित प्रश्न
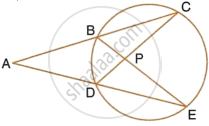
In the following figure; If AB = AC then prove that BQ = CQ.

From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
In the following figure, PQ and PR are tangents to the circle, with centre O. If `∠`QPR = 60°, calculate:
- ∠QOR,
- ∠OQR,
- ∠QSR.
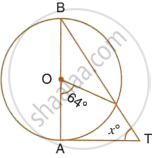
In the given figure, AB is the diameter of the circle, with centre O, and AT is the tangent. Calculate the numerical value of x.
In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
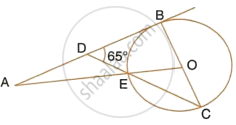
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
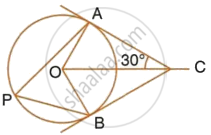
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°, find:
- ∠BCO
- ∠AOB
- ∠APB
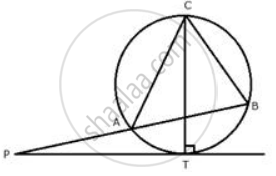
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ: