Advertisements
Advertisements
प्रश्न
In the given figure, AB is the diameter of the circle, with centre O, and AT is the tangent. Calculate the numerical value of x.
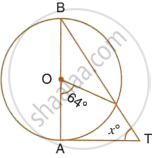
उत्तर
In ΔOBC,
OB = OC ...(Radii of the same circle)
∴ ∠OBC = ∠OCB
But, Ext. ∠COA = ∠OBC + ∠OCB
Ext. ∠COA = 2∠OBC
`=>` 64° = 2∠OBC
∴ ∠OBC = `64^circ/2` = 32°
Now in ΔABT,
∠BAT = 90° ...(OA ⊥ AT)
∠OBC or ∠ABT = 32°
∴ ∠BAT + ∠ABT + x° = 180°
`=>` 90° + 32° + x° = 180°
`=>` 122° + x° = 180°
`=>` x° = 180° – 122°
`=>` x° = 58°
APPEARS IN
संबंधित प्रश्न
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
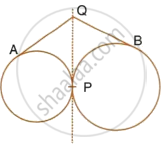
In the following figure; If AB = AC then prove that BQ = CQ.

In the following figure, PQ and PR are tangents to the circle, with centre O. If `∠`QPR = 60°, calculate:
- ∠QOR,
- ∠OQR,
- ∠QSR.
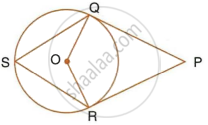
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
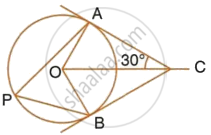
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°, find:
- ∠BCO
- ∠AOB
- ∠APB
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

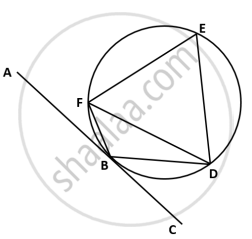
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
