Advertisements
Advertisements
प्रश्न
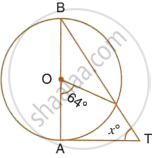
In the given figure, AB is the diameter of the circle, with centre O, and AT is the tangent. Calculate the numerical value of x.
उत्तर
In ΔOBC,
OB = OC ...(Radii of the same circle)
∴ ∠OBC = ∠OCB
But, Ext. ∠COA = ∠OBC + ∠OCB
Ext. ∠COA = 2∠OBC
`=>` 64° = 2∠OBC
∴ ∠OBC = `64^circ/2` = 32°
Now in ΔABT,
∠BAT = 90° ...(OA ⊥ AT)
∠OBC or ∠ABT = 32°
∴ ∠BAT + ∠ABT + x° = 180°
`=>` 90° + 32° + x° = 180°
`=>` 122° + x° = 180°
`=>` x° = 180° – 122°
`=>` x° = 58°
APPEARS IN
संबंधित प्रश्न
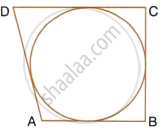
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
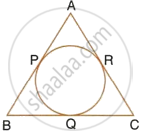
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
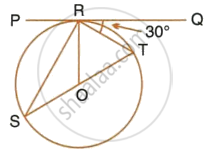
Given O is the centre of the circle and angle TRQ = 30°.
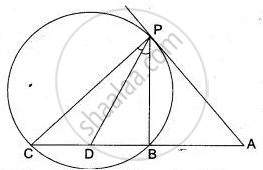
In Fig. AP is a tangent to the circle at P, ABC is secant and PD is the bisector of ∠BPC. Prove that ∠BPD = `1/2` (∠ABP - ∠APB).
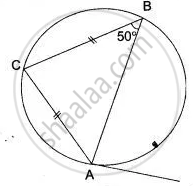
In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.
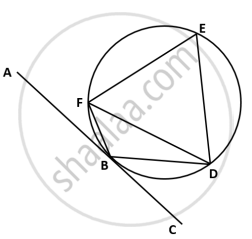
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
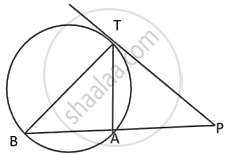
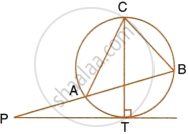
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.