Advertisements
Advertisements
प्रश्न
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
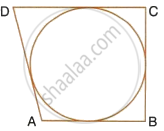
उत्तर
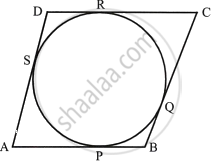
From A, AP and AS are tangents to the circle.
Therefore, AP = AS ...(i)
Similarly, we can prove that:
BP = BQ ...(ii)
CR = CQ ...(iii)
DR = DS ...(iv)
Adding,
AP + BP + CR + DR = AS + DS + BQ + CQ
AB + CD = AD + BC
Hence, AB + CD = AD + BC.
But AB = CD and BC = AD ...(v) (Opposite sides of a ||gm)
Therefore, AB + AB = BC + BC
2AB = 2BC
AB = BC ...(vi)
From (v) and (vi)
AB = BC = CD = DA
Hence, ABCD is a rhombus.
APPEARS IN
संबंधित प्रश्न
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
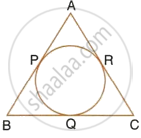
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
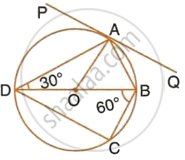
In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.
AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
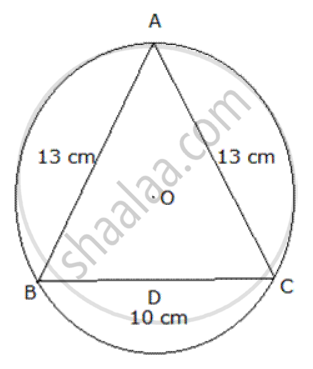
In figure , ABC is an isosceles triangle inscribed in a circle with centre O such that AB = AC = 13 cm and BC = 10 cm .Find the radius of the circle.
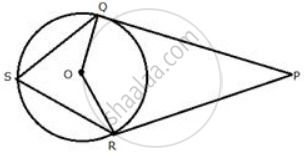
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ OQR
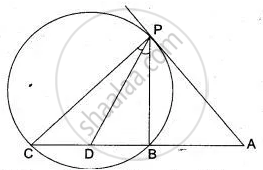
In Fig. AP is a tangent to the circle at P, ABC is secant and PD is the bisector of ∠BPC. Prove that ∠BPD = `1/2` (∠ABP - ∠APB).
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB