Advertisements
Advertisements
प्रश्न
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
उत्तर
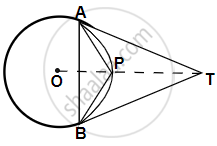
Join PB.
In ΔTAP and ΔTBP,
TA = TB ...(Tangents segments from an external points are equal in length)
Also, ∠ATP = ∠BTP. ...(Since OT is equally inclined with TA and TB)
TP = TP ...(Common)
`=>` ΔTAP ≅ ΔTBP ...(By SAS criterion of congruency)
`=>` ∠TAP = ∠TBP ...(Corresponding parts of congruent triangles are equal)
But ∠TBP = ∠BAP ...(Angles in alternate segments)
Therefore, ∠TAP = ∠BAP.
Hence, AP bisects ∠TAB.
APPEARS IN
संबंधित प्रश्न
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
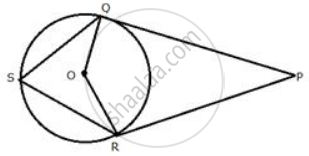
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ QSR
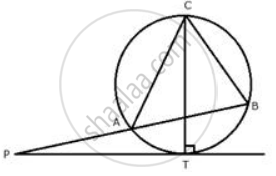
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
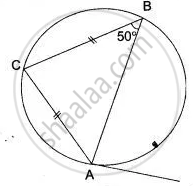
In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.
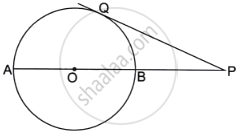
The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ: