Advertisements
Advertisements
प्रश्न
ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
उत्तर
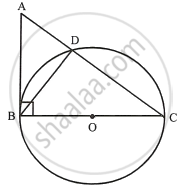
In ΔABC,
∠B = 90° and BC is the diameter of the circle.
Therefore, AB is the tangent to the circle at B.
Now, AB is tangent and ADC is the secant
∴ AB2 = AD × AC
APPEARS IN
संबंधित प्रश्न
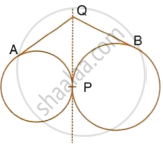
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
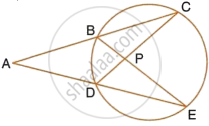
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
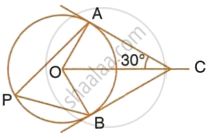
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°, find:
- ∠BCO
- ∠AOB
- ∠APB
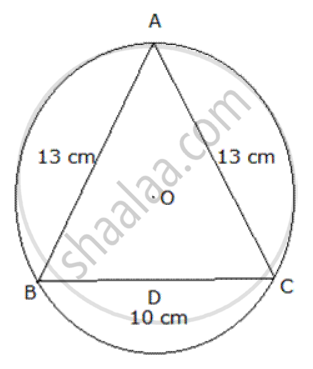
In figure , ABC is an isosceles triangle inscribed in a circle with centre O such that AB = AC = 13 cm and BC = 10 cm .Find the radius of the circle.
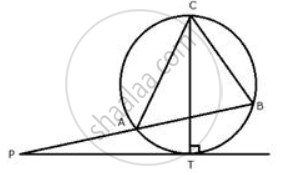
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
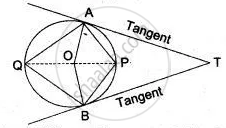
In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
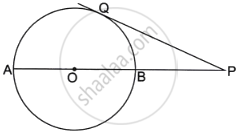
The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ: