Advertisements
Advertisements
प्रश्न
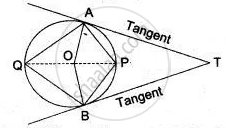
In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB
उत्तर
(i) ∠ AQP = ∠ PAT = 35° ....( Angles are in alternate segment)
(ii) ∠ BQP = ∠ PBT = 40° ....( Angles are in alternate segment)
(iii) ∠ AQB = ∠ AQP + ∠ BQP
∠ AQB = 35° + 40° = 75°
(iv) ∠ APB + ∠ AQB = 180° ....(Opposite ∠s of a cyclic quadrilateral are supplementary)
∴ ∠ APB + 75° = 180°
∴ ∠ APB = 105°
(v) ∠ AOB = 2∠ AQB = 2(75°) = 150° ....(Angle at the centre = 2 Angle at the circumference)
(vi) In quadrilateral AOBT:
∠ ATB = 360° - (∠OAT + ∠OBT + ∠AOB)
∠ ATB = 360° - (90° + 15° + 90°) = 30° ....(∠OAT = ∠OBT = 90° radius, ⊥ tangent).
APPEARS IN
संबंधित प्रश्न
The radius of a circle is 8 cm. calculate the length of a tangent draw to this circle from a point at a distance of 10 cm from its centre.
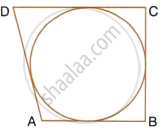
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
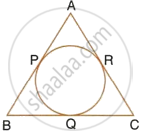
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
In quadrilateral ABCD; angles D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm, Find the radius of the circle.
AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
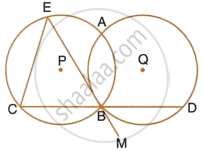
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
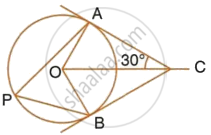
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°, find:
- ∠BCO
- ∠AOB
- ∠APB
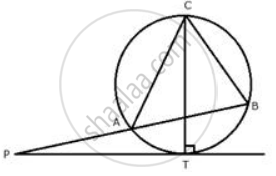
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT