Advertisements
Advertisements
प्रश्न
The radius of a circle is 8 cm. calculate the length of a tangent draw to this circle from a point at a distance of 10 cm from its centre.
उत्तर
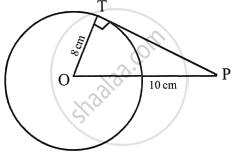
OP = 10 cm; radius OT = 8 cm
∵ OT ⊥ PT
In right ΔOTP,
OP2 = OT2 + PT2
102 = 82 + PT2
PT2 = 100 – 64
PT2 = 36
PT = 6
Length of tangent = 6 cm.
APPEARS IN
संबंधित प्रश्न
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
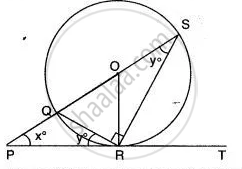
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

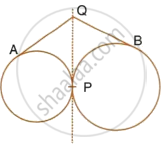
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
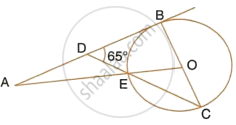
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

