Advertisements
Advertisements
प्रश्न
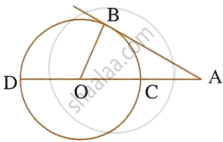
In the given figure, O is the center of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
उत्तर १
AB = 15 cm, AC = 7.5 cm
Let 'r' be the radius of the circle.
∴ OC = OB = r
AO = AC + OC = 7.5 + r
In ΔAOB,
AO2 = AB2 = OB2
(7.5 + r)2 = 152 + r2
`=> ((15 + 2r)/2)^2 = 225 + r^2`
`=>` 225 + 4r2 + 60r = 900 + 4r2
`=>` 60r = 675
`=>` r = 11.25 cm
Therefore, r = 11.25 cm
उत्तर २
AB2 = AC × AD ...(PT2 = PA × PB)
`=>` 152 = 7.5 × AD
`=>` AD = `225/7.5` = 30
`=>` CD = AD – AC
= 30 – 7.5
= 22.5
∴ Radius = `1/2` × CD
Radius = `1/2` × 22.5
Radius = 11.25 cm
APPEARS IN
संबंधित प्रश्न
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
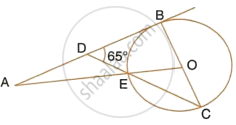
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
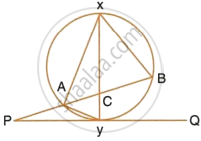
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
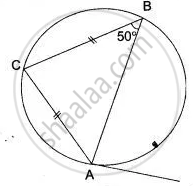
In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.