Advertisements
Advertisements
प्रश्न
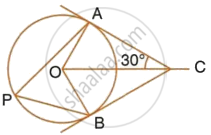
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°, find:
- ∠BCO
- ∠AOB
- ∠APB
उत्तर
In the given fig, O is the centre of the circle and CA and CB are the tangents to the circle from C. Also, ∠ACO = 30°
P is any point on the circle. PA and PB are joined.
To find:
- ∠BCO
- ∠AOB
- ∠APB
Proof:
i. In ΔOAC and OBC
OC = OC ...(Common)
OA = OB ...(Radius of the circle)
CA = CB ...(Tangents to the circle)
∴ ΔOAC ≅ ΔOBC ...(SSS congruence criterion)
∴ ∠ACO = ∠BCO = 30°
ii. ∠ACB = 30° + 30° = 60°
∴ ∠AOB + ∠ACB = 180°
`=>` ∠AOB + 60° = 180°
`=>` ∠AOB = 180° – 60°
`=>` ∠AOB = 120°
iii. Arc AB subtends ∠AOB at the centre and ∠APB is in the remaining part of the circle.
∴ `∠APB = 1/2 ∠AOB`
= `1/2 xx 120^circ`
= 60°
APPEARS IN
संबंधित प्रश्न
In the given figure, O is the center of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
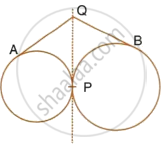
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
In the following figure, PQ and PR are tangents to the circle, with centre O. If `∠`QPR = 60°, calculate:
- ∠QOR,
- ∠OQR,
- ∠QSR.
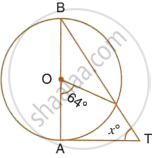
In the given figure, AB is the diameter of the circle, with centre O, and AT is the tangent. Calculate the numerical value of x.
In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

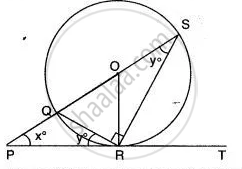
In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°
In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.