Advertisements
Advertisements
Question
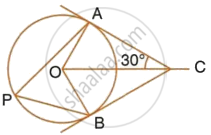
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°, find:
- ∠BCO
- ∠AOB
- ∠APB
Solution
In the given fig, O is the centre of the circle and CA and CB are the tangents to the circle from C. Also, ∠ACO = 30°
P is any point on the circle. PA and PB are joined.
To find:
- ∠BCO
- ∠AOB
- ∠APB
Proof:
i. In ΔOAC and OBC
OC = OC ...(Common)
OA = OB ...(Radius of the circle)
CA = CB ...(Tangents to the circle)
∴ ΔOAC ≅ ΔOBC ...(SSS congruence criterion)
∴ ∠ACO = ∠BCO = 30°
ii. ∠ACB = 30° + 30° = 60°
∴ ∠AOB + ∠ACB = 180°
`=>` ∠AOB + 60° = 180°
`=>` ∠AOB = 180° – 60°
`=>` ∠AOB = 120°
iii. Arc AB subtends ∠AOB at the centre and ∠APB is in the remaining part of the circle.
∴ `∠APB = 1/2 ∠AOB`
= `1/2 xx 120^circ`
= 60°
APPEARS IN
RELATED QUESTIONS
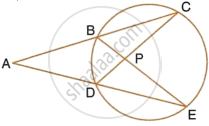
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
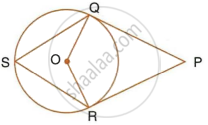
In the following figure, PQ and PR are tangents to the circle, with centre O. If `∠`QPR = 60°, calculate:
- ∠QOR,
- ∠OQR,
- ∠QSR.
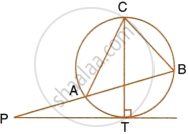
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
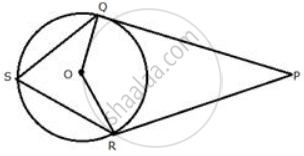
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ OQR
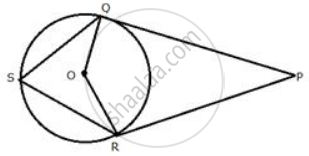
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ QSR
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

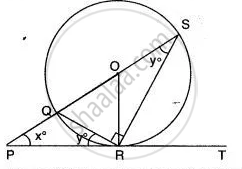
In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°
In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ: