Advertisements
Advertisements
Question
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
Solution
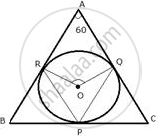
The incircle touches the sides of the triangle ABC and OP ⊥ BC, OQ ⊥ AC, OR ⊥ AB
i. In quadrilateral AROQ,
∠ORA = 90°, ∠OQA = 90°, ∠A = 60°
∠QOR = 360° – (90° + 90° + 60°)
∠QOR = 360° – 240°
∠QOR = 120°
ii. Now arc RQ subtends ∠QOR at the centre and ∠QPR at the remaining part of the circle.
∴ `∠QPR = 1/2 ∠QOR`
`=> ∠QPR = 1/2 xx 120^circ`
`=>` ∠QPR = 60°
APPEARS IN
RELATED QUESTIONS
From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
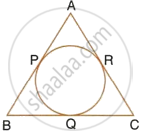
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
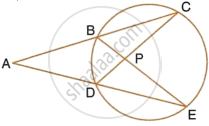
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
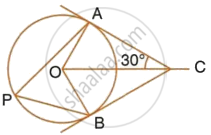
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°, find:
- ∠BCO
- ∠AOB
- ∠APB
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ QSR
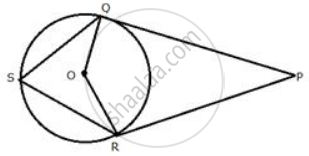
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
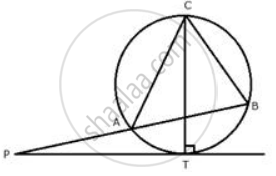
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
