Advertisements
Advertisements
Question
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
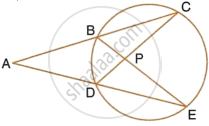
Solution
In ΔADC and ΔABE,
∠ACD = ∠AEB ...(Angles in the same segment)
AC = AE ...(Given)
∠A = ∠A ...(Common)
∴ ΔADC ≅ ΔABE ...(ASA postulate)
But AC = AE
∴ AC – AB = AE – AD
In ΔBPC and ΔDPE
∠C = ∠E ...(Angles in the same segment)
BC = DE
∠CBP = ∠CDE ...(Angles in the same segment)
∴ ΔBPC ≅ ΔDPE ...(ASA Postulate)
APPEARS IN
RELATED QUESTIONS
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
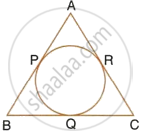
Also show that : AP + BQ + CR =
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)
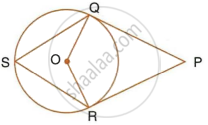
In the following figure, PQ and PR are tangents to the circle, with centre O. If
- ∠QOR,
- ∠OQR,
- ∠QSR.
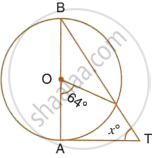
In the given figure, AB is the diameter of the circle, with centre O, and AT is the tangent. Calculate the numerical value of x.
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

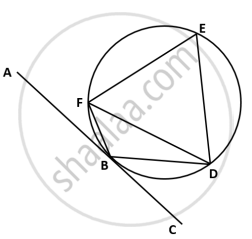
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
