Advertisements
Advertisements
Question
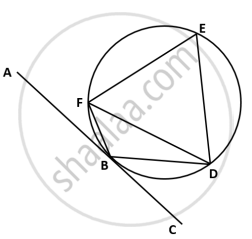
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
Solution
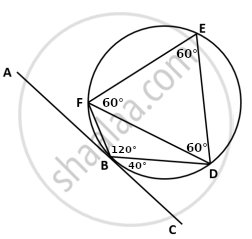
Given - In Diagram, ∆FED is an equilateral triangle, ∠CBD = 40°
To Find -
- ∠BFD,
- ∠FBD,
- ∠ABF
(a) ∠BFD = ∠CBD = 40° ....[Alternate segment theorem]
(b) ∠FBD is opposite to ∠FED.
So, It is a cyclic Quadrilateral. So, ∠FBD and ∠FED will be Supplementary to each other.
∴ ∠FBD + ∠FED = 180° ....[Cyclic Quadrilateral]
∠FBD + 60° = 180°
∠FBD = 180° - 60°
∠FBD = 120°
(c) AC is a line segment.
So, ∠ABF = 180° - (120° + 40°) ....[Line Segment]
∠ABF = 180° - 100°
∠ABF = 20°
APPEARS IN
RELATED QUESTIONS
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

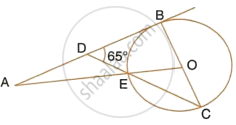
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
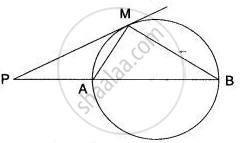
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2
A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB