Advertisements
Advertisements
Question
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
Solution
Given: A circle with centre O touches the sides AB, BC, CD and DA of a quadrilateral ABCD at the points P, Q, R and S respectively.
To Prove: ∠ AOB + ∠ COD = 180° and ∠ AOD + ∠BOC = 180°.
Construction: Join OP, OQ, OR and OS.
Proof: Since the two tangents drawn from an external point to a circle subtends equal angles at centre.
∴ ∠1 = ∠2, ∠3 = ∠4, ∠5 = ∠6 and ∠7 = ∠8 ...(i)
Now,
∠1 +∠2 +∠3 + ∠4 +∠5 +∠6 +∠7 +∠8 = 360° ...(Sum of all the angles subtended at a point is 360°)
⇒ 2(∠2 + ∠3 + ∠6 + ∠7) = 360° and 2(∠1 +∠8 + ∠4 +∠5) = 360°
⇒ (∠2 + ∠3) + (∠6 + ∠7) = 180° and (∠1 +∠8) + (∠4 +∠5) = 180°
⇒ ∠AOB + ∠COD = 180° ...(∵∠2 + ∠3 =∠AOB, ∠6 + ∠7 = ∠COD, ∠1 +∠8 = ∠AOD and ∠4 +∠5 = ∠BOC)
and ∠AOD + ∠BOC = 180°
APPEARS IN
RELATED QUESTIONS
In the following figure; If AB = AC then prove that BQ = CQ.

In quadrilateral ABCD; angles D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm, Find the radius of the circle.
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ OQR
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

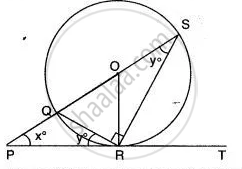
In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ:
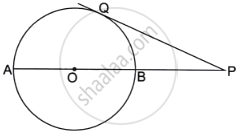
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.