Advertisements
Advertisements
Question
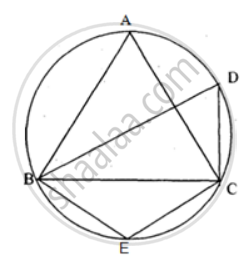
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
Solution
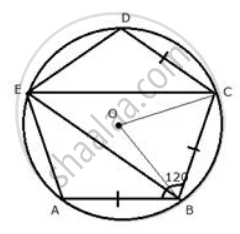
In cyclic quadrilateral BCDE,
∠ BED + ∠ BCD = 180°
⇒ ∠ BED + 120° = 180°
∴ ∠ BED = 60°
APPEARS IN
RELATED QUESTIONS
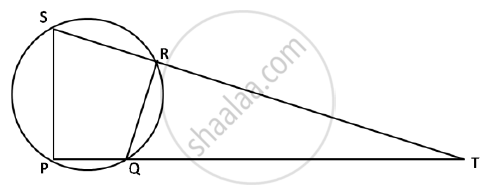
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T
1) Prove ΔTPS ~ ΔTRQ.
2) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm
3) Find the area of quadrilateral PQRS if the area of ΔPTS = 27 cm2.
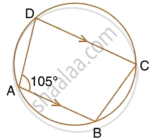
In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
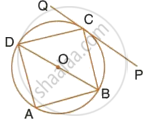
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠ CAB = 34° , find : ∠ CQB
In the figure, given below, find: ∠ADC, Show steps of your working.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

