Advertisements
Advertisements
प्रश्न
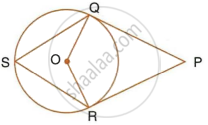
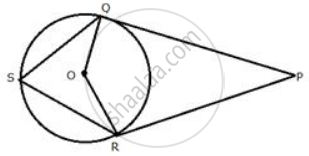
In the following figure, PQ and PR are tangents to the circle, with centre O. If `∠`QPR = 60°, calculate:
- ∠QOR,
- ∠OQR,
- ∠QSR.
उत्तर
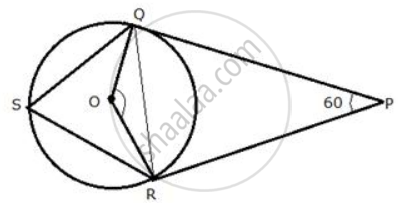
Join QR.
i. In quadrilateral ORPQ,
OQ ⊥ OP, OR ⊥ RP
∴ ∠OQP = 90°, ∠ORP = 90°, ∠QPR = 60°
∠QOR = 360° – (90° + 90° + 60°)
∠QOR = 360° – 240°
∠QOR = 120°
ii. In ΔQOR,
OQ = QR ...(Radii of the same circle)
∴ ∠OQR = ∠QRO ...(i)
But, ∠OQR + ∠QRO + ∠QOR = 180°
∠OQR + ∠ QRO + 120° = 180°
∠OQR + ∠QRO = 60°
From (i)
2∠OQR = 60°
∠OQR = 30°
iii. Now arc RQ subtends ∠QOR at the centre and ∠QSR at the remaining part of the circle.
∴ `∠QSR = 1/2 ∠QOR`
`=> ∠QSR = 1/2 xx 120^circ`
`=>` ∠QSR = 60°
APPEARS IN
संबंधित प्रश्न
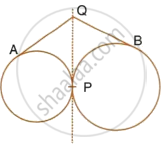
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
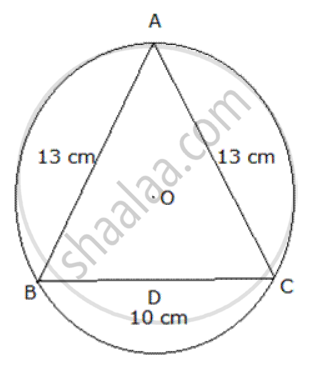
In figure , ABC is an isosceles triangle inscribed in a circle with centre O such that AB = AC = 13 cm and BC = 10 cm .Find the radius of the circle.
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ QSR
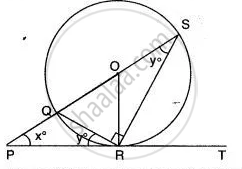
In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°
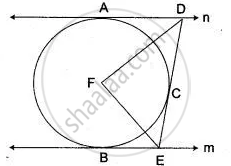
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

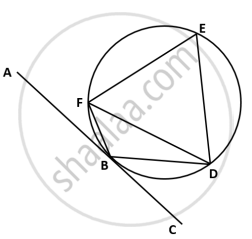
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
