Advertisements
Advertisements
Question
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
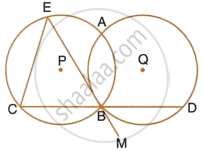
Solution
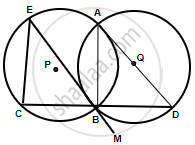
Join AB and AD
EBM is a tangent and BD is a chord.
∠DBM = ∠BAD ...(Angles in alternate segments)
But, ∠DBM = ∠CBE ...(Vertically opposite angles)
∴ ∠BAD = ∠CBE
Since in the same circle or congruent circles, if angles are equal, then chords opposite to them are also equal.
Therefore, CE = BD
APPEARS IN
RELATED QUESTIONS
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
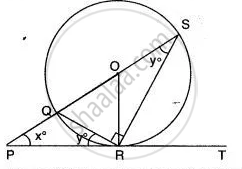
If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
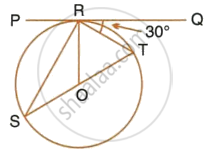
Given O is the centre of the circle and angle TRQ = 30°.
Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB