Advertisements
Advertisements
Question
If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
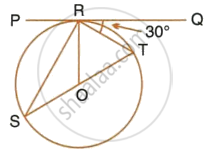
Given O is the centre of the circle and angle TRQ = 30°.
Solution
PQ is a tangent and OR is the radius.
∴ OR ⊥ PQ
∴ ∠ORT = 90°
`=>` ∠TRQ = 90° – 30° = 60°
But in ΔOTR,
OT = OR ...(Radii of the same circle)
∴ ∠OTR = 60° Or ∠STR = 60°
But,
∠PRS = ∠STR = 60 ...(Angle in the alternate segment)
In ΔORT,
∠ORT = 60°
∠OTR = 60°
∴ ∠ROT = 180° – (60° + 60°)
∴ ∠ROT = 180° – 120° = 60°
APPEARS IN
RELATED QUESTIONS
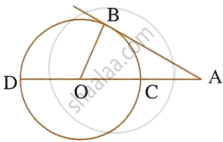
In the given figure, O is the center of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
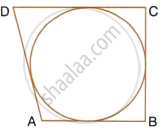
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

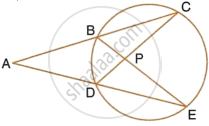
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
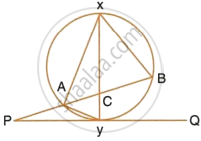
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ OQR
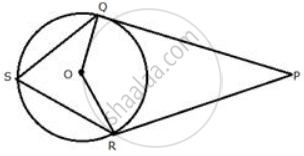
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
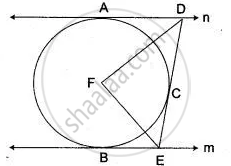
In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB
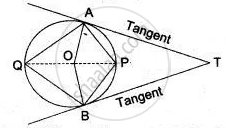
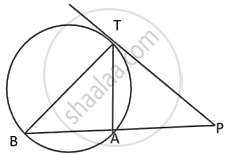
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.