Advertisements
Advertisements
प्रश्न
If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
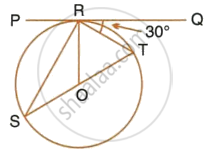
Given O is the centre of the circle and angle TRQ = 30°.
उत्तर
PQ is a tangent and OR is the radius.
∴ OR ⊥ PQ
∴ ∠ORT = 90°
`=>` ∠TRQ = 90° – 30° = 60°
But in ΔOTR,
OT = OR ...(Radii of the same circle)
∴ ∠OTR = 60° Or ∠STR = 60°
But,
∠PRS = ∠STR = 60 ...(Angle in the alternate segment)
In ΔORT,
∠ORT = 60°
∠OTR = 60°
∴ ∠ROT = 180° – (60° + 60°)
∴ ∠ROT = 180° – 120° = 60°
APPEARS IN
संबंधित प्रश्न
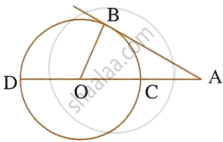
In the given figure, O is the center of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
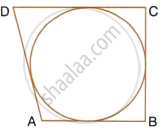
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
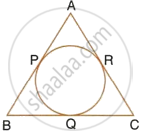
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
In the following figure; If AB = AC then prove that BQ = CQ.

From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
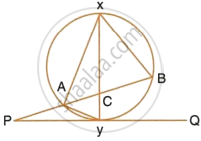
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

