Advertisements
Advertisements
प्रश्न
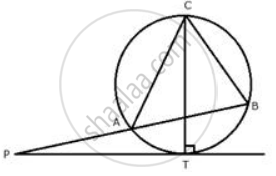
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

उत्तर
i. PA is the tangent and AB is a chord
∴ ∠PAB = ∠C ...(i) (Angles in the alternate segment)
AD is the bisector of ∠BAC
∴ ∠1 = ∠2 ...(ii)
In ΔADC,
Ext. ∠ADP = ∠C + ∠1
`=>` Ext ∠ADP = ∠PAB + ∠2 = ∠PAD
Therefore, ΔPAD is an isosceles triangle.
ii. In ΔABC,
Ext. ∠PBA = ∠C + ∠BAC
∴ ∠BAC = ∠PBA – ∠C
`=>` ∠1 + ∠2 = ∠PBA – ∠PAB ...(From (i) part)
`=>` 2∠1 = ∠PBA – ∠PAB
`=> ∠1 = 1/2 (∠PBA - ∠PAB)`
`=> ∠CAD = 1/2 (∠PBA - ∠PAB)`
APPEARS IN
संबंधित प्रश्न
From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
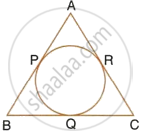
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
In quadrilateral ABCD; angles D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm, Find the radius of the circle.
AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
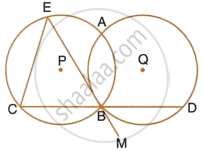
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
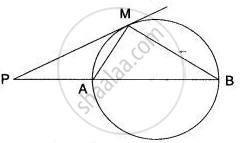
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2
In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

