Advertisements
Advertisements
Question
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
- ∠DAB,
- ∠BDC.

Solution

i. ∠DAB = ∠BED = 65°
(Angle subtended by the same chord on the circle are equal)
ii. ∠ADB = 90°
(Angle in a semicircle is a right angle)
∴ ∠ABD = 90° – ∠DAB = 90° – 65° = 25°
AB || DC
∴ ∠BDC = ∠ABD = 25° (Alternate angles)
APPEARS IN
RELATED QUESTIONS
Calculate the area of the shaded region, if the diameter of the semicircle is equal to 14 cm. Take `pi = 22/7`

Prove that the parallelogram, inscribed in a circle, is a rectangle.
Prove that the rhombus, inscribed in a circle, is a square.
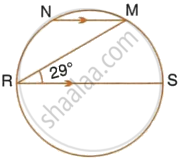
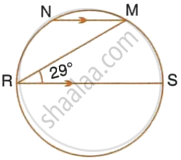
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠RNM
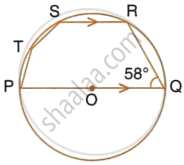
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°,
Calculate:
- ∠RPQ,
- ∠STP.
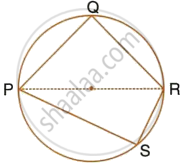
The following figure shows a circle with PR as its diameter. If PQ = 7 cm and QR = 3RS = 6 cm, find the perimeter of the cyclic quadrilateral PQRS.
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠NRM
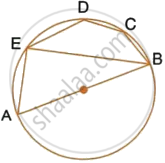
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate : ∠BCD.
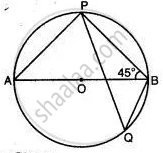
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.
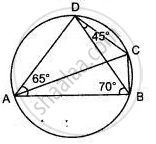
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.