Advertisements
Advertisements
प्रश्न
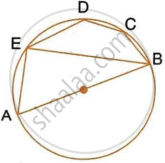
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
- ∠DAB,
- ∠BDC.

उत्तर

i. ∠DAB = ∠BED = 65°
(Angle subtended by the same chord on the circle are equal)
ii. ∠ADB = 90°
(Angle in a semicircle is a right angle)
∴ ∠ABD = 90° – ∠DAB = 90° – 65° = 25°
AB || DC
∴ ∠BDC = ∠ABD = 25° (Alternate angles)
APPEARS IN
संबंधित प्रश्न
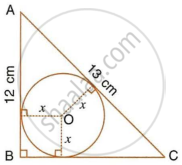
ABC is a right angles triangle with AB = 12 cm and AC = 13 cm. A circle, with centre O, has been inscribed inside the triangle.
Calculate the value of x, the radius of the inscribed circle.
Prove that the rhombus, inscribed in a circle, is a square.
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°.
Calculate:
- ∠EBA,
- ∠BCD.
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBA
Also, show that the ΔAOD is an equilateral triangle.
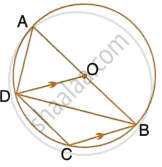
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠ADC
Also, show that the ΔAOD is an equilateral triangle.
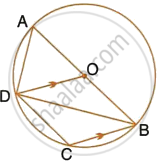
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.
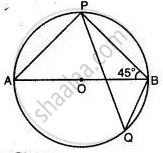
In the figure, ∠DBC = 58°. BD is diameter of the circle.
Calculate:
- ∠BDC
- ∠BEC
- ∠BAC
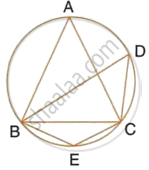
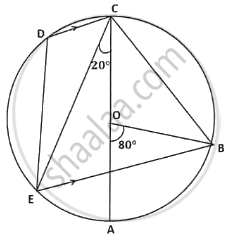
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED