Advertisements
Advertisements
Question
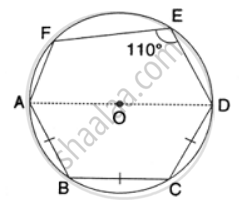
In the following figure, AD is the diameter of the circle with centre O. chords AB, BC and CD are equal. If ∠DEF = 110°, Calculate: ∠FAB.
Solution
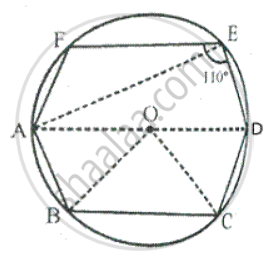
Join AE , OB and OC
∵ Chord AB = Chord BC = Chord CD ...[given]
∴ ∠AOB = ∠BOC = ∠COD ...(Equal chords subtends equal angles at the centre)
But ∠AOB + ∠BOC + ∠COD = 180° ...[AOD is a straight line ]
∠AOB = ∠BOC = ∠COD = 60°
In ∠OAB, OA = OB
∴ ∠OAB = ∠OBA ...[radii of the same circle]
But ∠OAB + ∠OBA = 180° − AOB
= 180° − 60°
= 120°
∴ ∠OAB = ∠OBA = 60°
In cyclic quadrilateral ADEF,
∠DEF + ∠DAF = 180°
⇒ ∠DAF = 180° − ∠DEF
= 180° − 110°
= 70°
Now, ∠FAB = ∠DAF + ∠OAB
= 70° + 60°
= 130°
APPEARS IN
RELATED QUESTIONS
Prove that the parallelogram, inscribed in a circle, is a rectangle.
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate: ∠AEF
Using ruler and a compass only construct a semi-circle with diameter BC = 7cm. Locate a point A on the circumference of the semicircle such that A is equidistant from B and C. Complete the cyclic quadrilateral ABCD, such that D is equidistant from AB and BC. Measure ∠ADC and write it down.
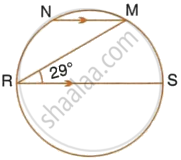
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠NRM
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBA
Also, show that the ΔAOD is an equilateral triangle.
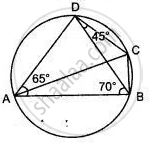
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.
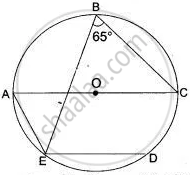
In Fig, Chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, Calculate ∠ DEC.
In the figure given alongside, AD is the diameter of the circle. If ∠ BCD = 130°, Calculate: (i) ∠ DAB (ii) ∠ ADB.
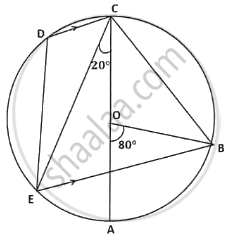
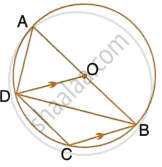
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED