Advertisements
Advertisements
Question
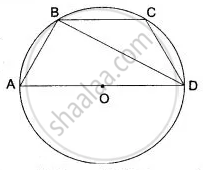
In the figure given alongside, AD is the diameter of the circle. If ∠ BCD = 130°, Calculate: (i) ∠ DAB (ii) ∠ ADB.
Solution
(i) Since ABCD is a cyclic quadrilateral.
∴ Its Opposite angles are supplementary.
∴ ∠ DAB + ∠ BCD = 180°
⇒ ∠ DAB = 180° - ∠ BCD
⇒ ∠ DAB = 180° - 130°
⇒ ∠ DAB = 50°
(ii) Since, angle in the semicircle is a right angle.
∴ In Δ ABD, ∠ABD = 90°
Since, the sum of the angle of a triangle is 180°
∴ ∠ABD + ∠ADB + ∠ DAB = 180°
∴ 90° + ∠ADB + 50° = 180°
∠ADB = 180° - (90° + 50°)
∠ADB = 180° - 140°
∠ADB = 40°
APPEARS IN
RELATED QUESTIONS
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
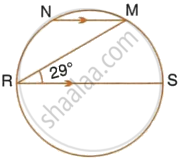
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠RNM
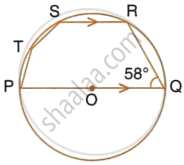
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°,
Calculate:
- ∠RPQ,
- ∠STP.
The following figure shows a circle with PR as its diameter. If PQ = 7 cm and QR = 3RS = 6 cm, find the perimeter of the cyclic quadrilateral PQRS.
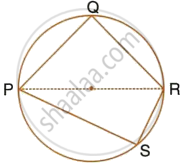
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBC
Also, show that the ΔAOD is an equilateral triangle.

In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠ADC
Also, show that the ΔAOD is an equilateral triangle.
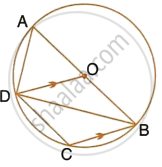
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.
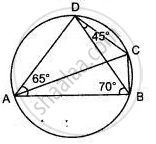
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.
In Fig, Chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, Calculate ∠ DEC.
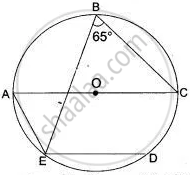
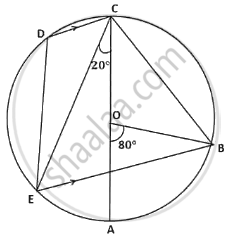
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED