Advertisements
Advertisements
Question
If two sides of a cyclic quadrilateral are parallel; prove that:
- its other two sides are equal.
- its diagonals are equal.
Solution
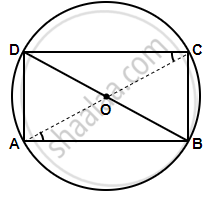
Given:
ABCD is a cyclic quadrilateral in which AB || DC. AC and BD are its diagonals.
To prove:
- AD = BC
- AC = BD
Proof:
i. AB || DC `=>` ∠DCA = ∠CAB ...[Alternate angles]
Now, chord AD subtends ∠DCA and chord BC subtends ∠CAB
At the circumference of the circle.
∴ ∠DCA = ∠CAB ...[Proved]
∴ Chord AD = Chord BC or AD = BC
ii. Now in ΔABC and ΔADB,
AB = AB ...[Common]
∠ACB = ∠ADB ...[Angles in the same segment]
BC = AD ...[Proved]
By Side – Angle – Side criterion of congruence, we have
ΔACB ≅ ΔADB ...[SAS postulate]
The corresponding parts of the congruent triangles are congruent.
∴ AC = BD ...[c.p.c.t]
APPEARS IN
RELATED QUESTIONS
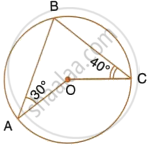
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. Find ∠AOC . Show your steps of working.
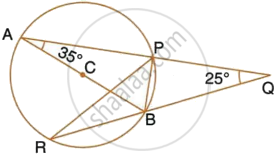
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PRB
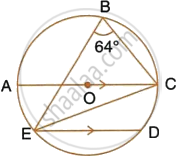
In the given figure, AOC is a diameter and AC is parallel to ED. If ∠CBE = 64°, calculate ∠DEC.
In the given circle with diameter AB, find the value of x.
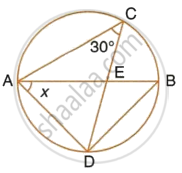
In cyclic quadrilateral ABCD; AD = BC, ∠BAC = 30° and ∠CBD = 70°; find:
- ∠BCD
- ∠BCA
- ∠ABC
- ∠ADC
In the given figure, ∠ACE = 43° and ∠CAF = 62°; find the values of a, b and c.

In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in ∠ABC.

AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PBR
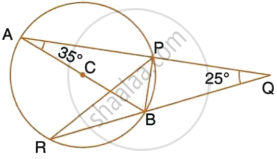
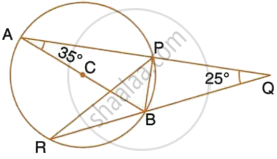
AB is a diameter of the circle APBR, as shown in the figure. APQ and RBQ are straight lines. Find : ∠BPR
In the given below the figure, AB is parallel to DC, ∠BCD = 80° and ∠BAC = 25°, Find
(i) ∠CAD, (ii) ∠CBD, (iii) ∠ADC.

