Advertisements
Advertisements
Question
In the given below the figure, AB is parallel to DC, ∠BCD = 80° and ∠BAC = 25°, Find
(i) ∠CAD, (ii) ∠CBD, (iii) ∠ADC.

Solution
(i) ∠CAD = ∠BCE - ∠CAB
∴ ∠CAD = 80° - 25°
∴ ∠CAD = 55°
∵ Ext. of cyclic is equal to opp. int
(ii) ∠CBD = ∠CAD = 55° ...(Angles in the same segment)
(iii) ∠ ADC = 180° - ∠ DAB
∴ ∠ ADC = 180° - 80°
∴ ∠ ADC = 100°.
APPEARS IN
RELATED QUESTIONS
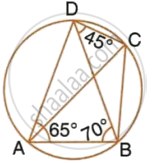
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
- Prove that AC is a diameter of the circle.
- Find ∠ACB.

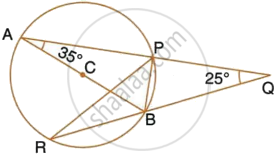
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PRB
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find:
- ∠BCD
- ∠ACB
Hence, show that AC is a diameter.
The given figure shows a circle with centre O and ∠ABP = 42°.

Calculate the measure of:
- ∠PQB
- ∠QPB + ∠PBQ
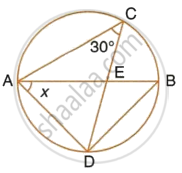
In the given circle with diameter AB, find the value of x.
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.

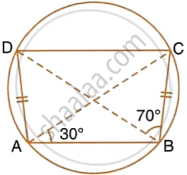
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°.
Find:
- ∠BCD
- ∠BCA
- ∠ABC
- ∠ADB
In the figure, AB = AC = CD, ∠ADC = 38°. Calculate: (i) ∠ ABC, (ii) ∠ BEC.
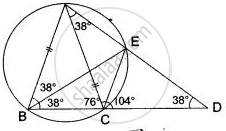
In the given figure, ∠CAB = 25°, find ∠BDC, ∠DBA and ∠COB
In the given figure (drawn not to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.
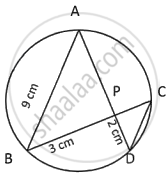
- Prove that ΔAPB ~ ΔCPD.
- Find the length of CD.
- Find area ΔAPB : area ΔCPD.
