Advertisements
Advertisements
Question
In the given figure, AOC is a diameter and AC is parallel to ED. If ∠CBE = 64°, calculate ∠DEC.
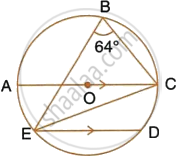
Solution

Join AB,
∠ABC = 90°
(Angle in a semi circle)
∴ ∠ABE = 90° – 64° = 26°
Now, ∠ABE = ∠ACE = 26°
(Angle in the same segment)
Also, AC || ED
∴ ∠DEC = ∠ACE = 26°
(Alternate angles)
APPEARS IN
RELATED QUESTIONS
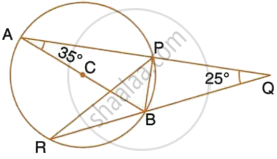
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PRB
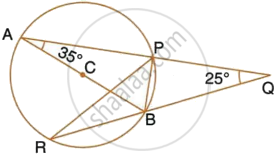
The given figure shows a circle with centre O and ∠ABP = 42°.

Calculate the measure of:
- ∠PQB
- ∠QPB + ∠PBQ
In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.
If two sides of a cyclic quadrilateral are parallel; prove that:
- its other two sides are equal.
- its diagonals are equal.
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.

In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in ∠ABC.

AB is a diameter of the circle APBR, as shown in the figure. APQ and RBQ are straight lines. Find : ∠BPR
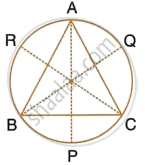
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that :
∠ACB = 2∠APR,
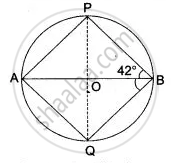
In the following figure, O is the centre of the circle, ∠ PBA = 42°.
Calculate:
(i) ∠ APB
(ii) ∠PQB
(iii) ∠ AQB
In the given figure, ∠CAB = 25°, find ∠BDC, ∠DBA and ∠COB
