Advertisements
Advertisements
Question
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate: ∠AEF
Advertisements
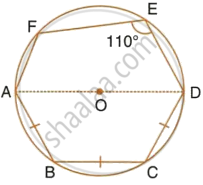
Solution
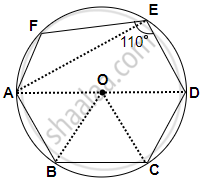
Join AE, OB and OC
∵ AOD is the diameter,
∴ ∠AED = 90° ...[Angle in a semi-circle]
But ∠DEF = 110° ...[Given]
∴ ∠AEF = ∠DEF – ∠AED
= 110° – 90°
= 20°
RELATED QUESTIONS
In the figure, m∠DBC = 58°. BD is the diameter of the circle. Calculate:
1) m∠BDC
2) m∠BEC
3) m∠BAC
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
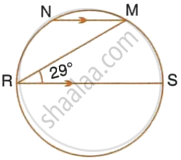
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠RNM
In the figure, given alongside, AB || CD and O is the centre of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.
Using ruler and a compass only construct a semi-circle with diameter BC = 7cm. Locate a point A on the circumference of the semicircle such that A is equidistant from B and C. Complete the cyclic quadrilateral ABCD, such that D is equidistant from AB and BC. Measure ∠ADC and write it down.
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate : ∠BCD.
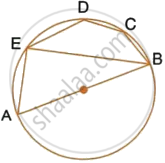
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBA
Also, show that the ΔAOD is an equilateral triangle.
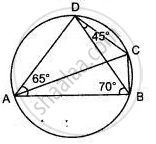
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.
In Fig, Chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, Calculate ∠ DEC.
