Advertisements
Advertisements
प्रश्न
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

उत्तर
i. Since PAT || BC
∴ ∠PAB = ∠ABC (Alternate angles) ...(i)
In cyclic quadrilateral ABCD,
Ext ∠ADQ = ∠ABC ...(ii)
From (i) and (ii)
∠PAB = ∠ADQ
ii. Arc AB subtends ∠AOB at the centre and ∠ADB at the remaining part of the circle.
∴ ∠AOB = 2∠ADB
`=>` ∠AOB = 2∠PAB ...(Angles in alternate segments)
`=>` ∠AOB = 2∠ADQ ...(Proved in (i) part)
iii. ∴ ∠BAP = ∠ADB ...(Angles in alternate segments)
But ∠BAP = ∠ADQ ...(Proved in (i) part)
∴ ∠ADQ = ∠ADB
APPEARS IN
संबंधित प्रश्न
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
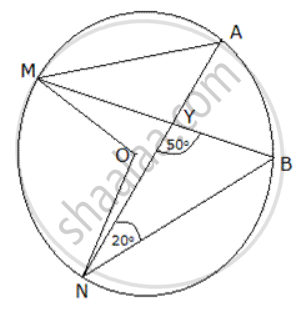
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
In following figure.,ABCD is a cyclic quadrilateral . If ∠ BCD = 100° and ∠ ABD = 70° , find ∠ ADB.
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.