Advertisements
Advertisements
Question
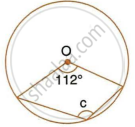
In the following figure, O is the centre of the circle. Find the values of a, b and c.
Solution
Here, `c = 1/2 ` Reflex (112°)
(Angle at the centre is double the angle at the circumference subtended by the same chord)
`=> c = 1/2 xx (360^circ - 112^circ) = 124^circ`
APPEARS IN
RELATED QUESTIONS
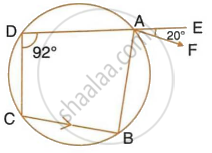
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
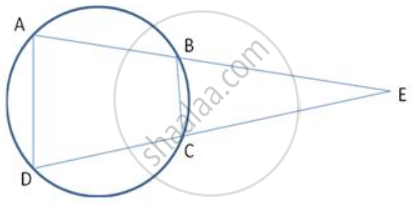
ABCD is a cyclic quadrilateral, AB and DC are produced to meet in E. Prove that ΔEBC ≅ ΔEDA.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In the following figure, Prove that AD is parallel to FE.

In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
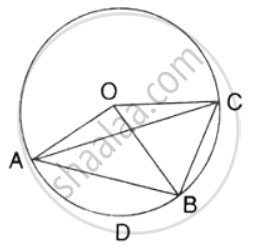
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

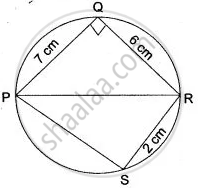
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.