Advertisements
Advertisements
Question
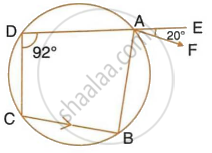
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
Solution
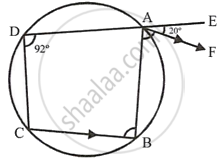
In cyclic quad. ABCD,
AF || CB and DA is produced to E such that ∠ADC = 92° and ∠FAE = 20°
Now, we need to find the measure of ∠BCD
In cyclic quad. ABCD,
`=>` ∠B + ∠D = 180°
`=>` ∠B + 92° = 180°
`=>` ∠B = 180° – 92°
`=>` ∠B = 88°
Since AF || CB, ∠FAB = ∠B = 88°
But, ∠FAE = 20° ...[Given]
Ext. ∠BAE = ∠BAF + ∠FAE
= 88° + 20°
= 108°
But, Ext. ∠BAE = ∠BCD
∴ ∠BCD = 108°
APPEARS IN
RELATED QUESTIONS
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

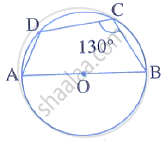
ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

ABCD is a cyclic quadrilateral AB and DC are produced to meet in E. Prove that Δ EBC ∼ Δ EDA.
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
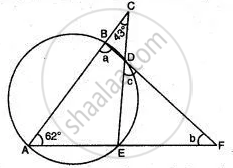
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.