Advertisements
Advertisements
Question
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
Solution
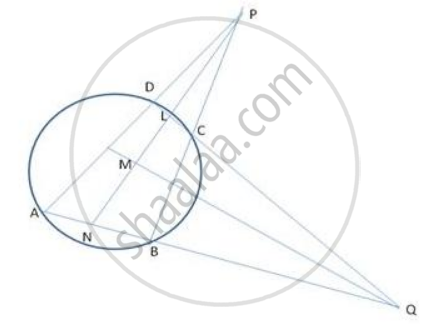
Here, ABCD is a cyclic quadrilateral. PM is bisector of ∠ APB and QM is bisector of ∠ AQD
In Δ PDL and Δ PBN, ∠ 1=∠ 2 (PM is a bisector of LP)
∠ 3 = ∠ 9 (exterior angle of cydic quad. = interior opposite angle)
∴ ∠ 4 = ∠ 7
But, ∠ 4 = ∠ 8 (vertical opposite angles)
∴ ∠ 7 = ∠ 8
Now in Δ QMN and Δ QML
∠ 7 = ∠ 8 (proved above)
∠ S = ∠ 6 (QM is bisector of Q)
∴ Δ QMN ~ Δ QML
⇒ ∠ QMN and ∠ QML
But, ∠ QMN + ∠ QML = 180°
∴ ∠ QMN = ∠ QML = 90°
Hence, ∠ PMQ = 90 °
APPEARS IN
RELATED QUESTIONS
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:
- ∠ONL + ∠OML = 180°
- ∠BAM + ∠BMA
- ALOB is a cyclic quadrilateral.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

ABCD is a cyclic quadrilateral AB and DC are produced to meet in E. Prove that Δ EBC ∼ Δ EDA.
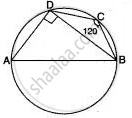
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
