Advertisements
Advertisements
Question
ABCD is a cyclic quadrilateral AB and DC are produced to meet in E. Prove that Δ EBC ∼ Δ EDA.
Solution
In Δ EBC and Δ EDA, we have
∠ EBC = ∠ EDA ...[ Exterior or angle in a cyclic quadrilateral is equal to opposite interior angle]
∠ ECB = ∠ EAD ...[ Exterior or angle in a cyclic quadrilateral is equal to opposite interior angle]
and ∠ E = ∠ E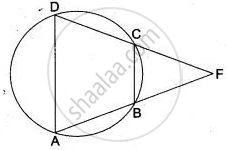
So, by AAA exterior of similarly, we get
Δ EBC ∼ Δ EDA
Hence proved.
APPEARS IN
RELATED QUESTIONS
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
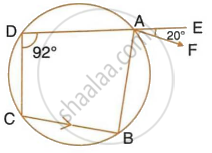
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
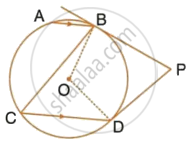
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
In the given figure, O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find:
- ∠BOD
- ∠BPD
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
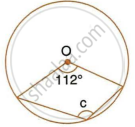
In the following figure, O is the centre of the circle. Find the values of a, b and c.
In the following figure, Prove that AD is parallel to FE.

If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
