Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral AB and DC are produced to meet in E. Prove that Δ EBC ∼ Δ EDA.
उत्तर
In Δ EBC and Δ EDA, we have
∠ EBC = ∠ EDA ...[ Exterior or angle in a cyclic quadrilateral is equal to opposite interior angle]
∠ ECB = ∠ EAD ...[ Exterior or angle in a cyclic quadrilateral is equal to opposite interior angle]
and ∠ E = ∠ E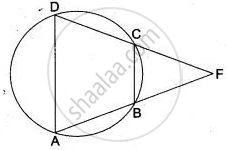
So, by AAA exterior of similarly, we get
Δ EBC ∼ Δ EDA
Hence proved.
APPEARS IN
संबंधित प्रश्न
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

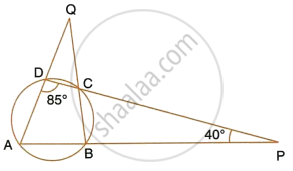
Use the given figure to find:
- ∠BAD,
- ∠DQB.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
In the figure, given below, find: ∠ABC. Show steps of your working.

In the following figure, Prove that AD is parallel to FE.

In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

