Advertisements
Advertisements
प्रश्न
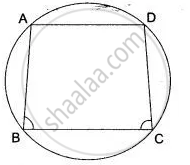
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
उत्तर
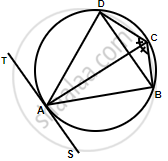
∠ADB = ∠ACB ...(i) (Angles in same segement)
Similarly,
∠ABD = ∠ACD ...(ii)
But, ∠ACB = ∠ACD ...(AC is bisector of ∠BCD)
∴ ∠ADB = ∠ABD ...(From (i) and (ii))
TAS is a tangent and AB is a chord
∴ ∠BAS = ∠ADB ...(Angles in alternate segment)
But, ∠ADB = ∠ABD
∴ ∠BAS = ∠ABD
But these are alternate angles
Therefore, TS || BD
APPEARS IN
संबंधित प्रश्न
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
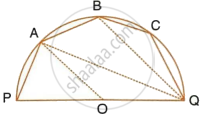
The given figure shows a semi-circle with centre O and diameter PQ. If PA = AB and ∠BCQ =140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
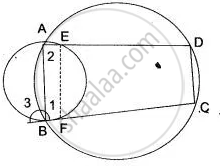
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
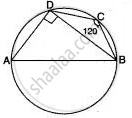
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA