Advertisements
Advertisements
प्रश्न
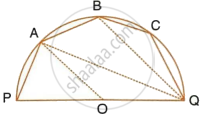
The given figure shows a semi-circle with centre O and diameter PQ. If PA = AB and ∠BCQ =140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
उत्तर
Join PB.
i. In cyclic quadrilateral PBCQ,
∠BPQ + ∠BCQ = 180°
`=>` ∠BPQ + 140° = 180°
`=>` ∠BPQ = 40° ...(1)
Now in ΔPBQ,
∠PBQ + ∠BPQ + ∠BQP = 180°
`=>` 90° + 40° + ∠BQP = 180°
`=>` ∠BQP = 50°
In cyclic quadrilateral PQBA,
∠PQB + ∠PAB = 180°
`=>` 50° + ∠PAB = 180°
`=>` ∠PAB = 130°
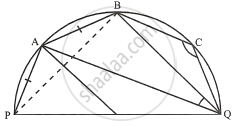
ii. Now in ΔPAB,
∠PAB + ∠APB + ∠ABP = 180°
`=>` 130° + ∠APB + ∠ABP = 180°
`=>` ∠APB + ∠ABP = 50°
But ∠APB = ∠ABP ...(∵ PA = PB)
∴ ∠APB = ∠ABP = 25°
∠BAQ = ∠BPQ = 40°
∠APB = 25° = ∠AQB ...(Angles in the same segment)
∴ ∠AQB = 25° ...(2)
iii. Arc AQ subtends ∠AOQ at the centre and ∠APQ at the remaining part of the circle.
We have,
∠APQ = ∠APB + ∠BPQ ...(3)
From (1), (2) and (3), we have
∠APQ = 25° + 40° = 65°
∴ ∠AOQ = 2∠APQ = 2 × 65° = 130°
Now in ΔAOQ,
∠OAQ = ∠OQA ...( ∵ OA = OQ)
But ∠OAQ + ∠OQA + ∠AOQ = 180°
`=>` ∠OAQ + ∠OAQ + 130° = 180°
`=>` 2∠OAQ = 50°
`=>` ∠OAQ = 25°
∴ ∠OAQ = ∠AQB
But these are alternate angles.
Hence, AO is parallel to BQ.
APPEARS IN
संबंधित प्रश्न
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
In following figure.,ABCD is a cyclic quadrilateral . If ∠ BCD = 100° and ∠ ABD = 70° , find ∠ ADB.
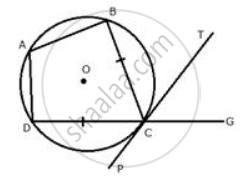
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.
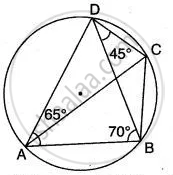
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.