Advertisements
Advertisements
प्रश्न
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ALOB is a cyclic quadrilateral.
उत्तर
ABCD is a square whose diagonals AC and BD intersect each other at right angles at O.
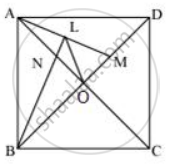
In quadrilateral ALOB,
∵ ∠ ABO + ∠ ALO = 45° + 90° + 45° = 180°
Therefore, ALOB is a cyclic quadrilateral.
APPEARS IN
संबंधित प्रश्न
How many tangents can a circle have?
In the given figure, find TP if AT = 16 cm and AB = 12 cm.

What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
Draw Δ ABC such that, AB = 8 cm, BC = 6 cm and ∠ B = 90°. Draw seg BD
perpendicular to hypotenuse AC. Draw a circle passing through points
B, D, A. Show that line CB is a tangent of the circle.
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
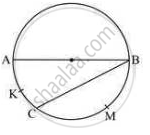
In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
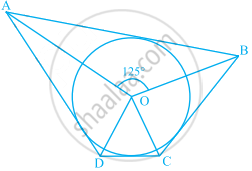
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
The tangents drawn at the extremities of the diameter of a circle are ______.
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
How many tangents can be drawn to a circle from a point on it?
