Advertisements
Advertisements
प्रश्न
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.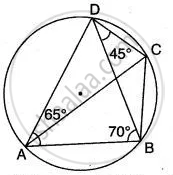
उत्तर
Given:
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
(i) Quadrilateral ABCD is cyclic quadrilateral.
∴ ∠ DAB + ∠ BCD = 180°
∴ 65° + ∠ BCD = 180°
∴ ∠ BCD = 180° - 65°
∴ ∠ BCD = 115°
(ii) In ΔADB,
∴ ∠ DAB + ∠ ABD + ∠ ADB = 180°
∴ 65° + 70° + ∠ ADB = 180°
∴ ∠ ADB = 180° - 135°
∴ ∠ ADB = 45°.
APPEARS IN
संबंधित प्रश्न
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T
1) Prove ΔTPS ~ ΔTRQ.
2) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm
3) Find the area of quadrilateral PQRS if the area of ΔPTS = 27 cm2.
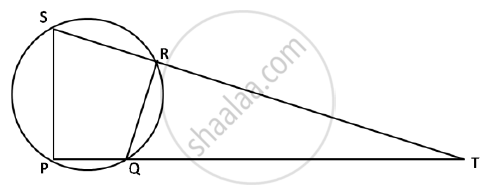
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
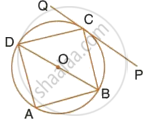
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In the following figure, Prove that AD is parallel to FE.

Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

