Advertisements
Advertisements
प्रश्न
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.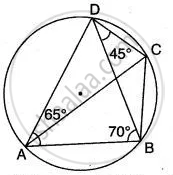
उत्तर
Given:
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
(i) Quadrilateral ABCD is cyclic quadrilateral.
∴ ∠ DAB + ∠ BCD = 180°
∴ 65° + ∠ BCD = 180°
∴ ∠ BCD = 180° - 65°
∴ ∠ BCD = 115°
(ii) In ΔADB,
∴ ∠ DAB + ∠ ABD + ∠ ADB = 180°
∴ 65° + 70° + ∠ ADB = 180°
∴ ∠ ADB = 180° - 135°
∴ ∠ ADB = 45°.
APPEARS IN
संबंधित प्रश्न
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

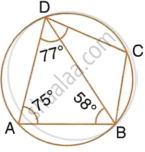
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

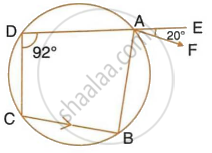
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
ABCD is a cyclic quadrilateral, AB and DC are produced to meet in E. Prove that ΔEBC ≅ ΔEDA.
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
In the figure, given below, find: ∠ABC. Show steps of your working.

In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC