Advertisements
Advertisements
प्रश्न
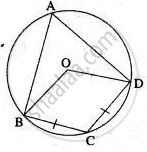
Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
उत्तर

ABCDE is a regular pentagon.
∴ `∠BAE = ∠ABC = ∠BCD = ∠CDE = ∠DEA = ((5 - 2)/5) xx 180^circ = 180^circ`
In ΔAED,
AE = ED ...(Sides of regular pentagon ABCDE)
∴ ∠EAD = ∠EDA
In ΔAED,
∠AED + ∠EAD + ∠EDA = 180°
`=>` 108° + ∠EAD + ∠EAD = 180°
`=>` 2∠EAD = 180° − 108° = 72°
`=>` ∠EAD = 36°
∴ ∠EDA = 36°
∠BAD = ∠BAE − ∠EAD = 108° − 36° = 72°
In quadrilateral ABCD,
∠BAD + ∠BCD = 108° + 72° = 180°
∴ ABCD is a cyclic quadrilateral
APPEARS IN
संबंधित प्रश्न
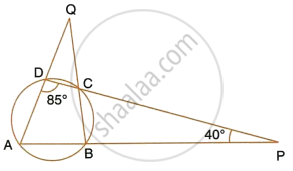
Use the given figure to find:
- ∠BAD,
- ∠DQB.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
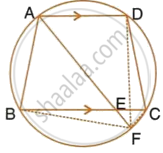
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
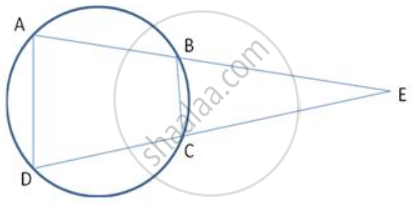
ABCD is a cyclic quadrilateral, AB and DC are produced to meet in E. Prove that ΔEBC ≅ ΔEDA.
In following figure.,ABCD is a cyclic quadrilateral . If ∠ BCD = 100° and ∠ ABD = 70° , find ∠ ADB.
In the following figure, Prove that AD is parallel to FE.

In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.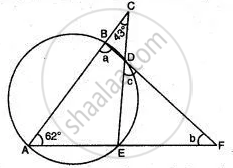
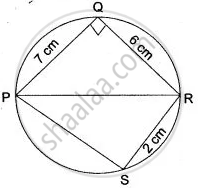
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.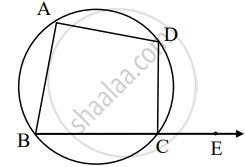
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
